1Discretization¶
In this section, we discuss important elements about discretizing Maxwell’s equations in the time-domain with the convolution term shown in eq. (9), to simulate IP effects in time-domain EM data. Appendix A.1 illustrates how convolutionary time-domain Maxwell’s equations can be discretized. Appendix A.2 describes how the singularity of SE conductivity function at is handled. Most of key challenges about this discretization are tackled in Marchant (2015) (see page 21), and we have extended his work, applied for Cole-Cole conductivity, to SE conductivity.
1.1Maxwell’s equations¶
The stretched exponential (SE) conductivity provided in eq. (8) in the time-domain can be rewritten as
where is a Dirac-Delta function and is
Considering a time-dependent conductivity, Ohm’s Law can be written as
and substituting eq. (1) yields
Using the Backward Euler method, we discretize Maxwell’s equations in eqs. (4) and (5) in time:
where . To discretize the integral in eq. (4), we use the trapezoidal rule:
Fig. 1 shows a conceptual diagram for this discrete convolution procedure. Hence eq. (4) can be discretized as
This can be rewritten as
where the polarization current, is
For the simplest case when (), then is well defined and and are respectively:
However, when , is singular and hence it requires special numerical treatment; this is described in Appendix A.2.
For the discretization, we use a staggered mimetic finite volume approach Hyman et al. (2002). Here, boldface with uppercase and lowercase indicate matrices and column vectors, respectively. Further details about the discretization can be found in Haber (2014) (see page 31). Discretizing eqs. (5), (6), and (9) yields
where
Here, is the discrete edge-curl operator; and are the edge and face inner-product matrices, respectively. For an inner-product matrix, the subscript indicates corresponding physical property (e.g. : the face inner-product matrix for ).
Rearranging the above equations to solve for yields:
By solving the above equation at each time step, we obtain . The measured data for AEM are often , which can be computed as
The measured data at a receiver loop can be expressed as
where is an interpolation matrix, which projects fields, defined in a 3D domain, to a receiver location, and samples those fields at the measured time channels. For discretization of eqs. ( 17) to ( 19) we use, SimPEG’s mesh toolbox. The developed code is open-source as a SimPEG-EMIP package (https://
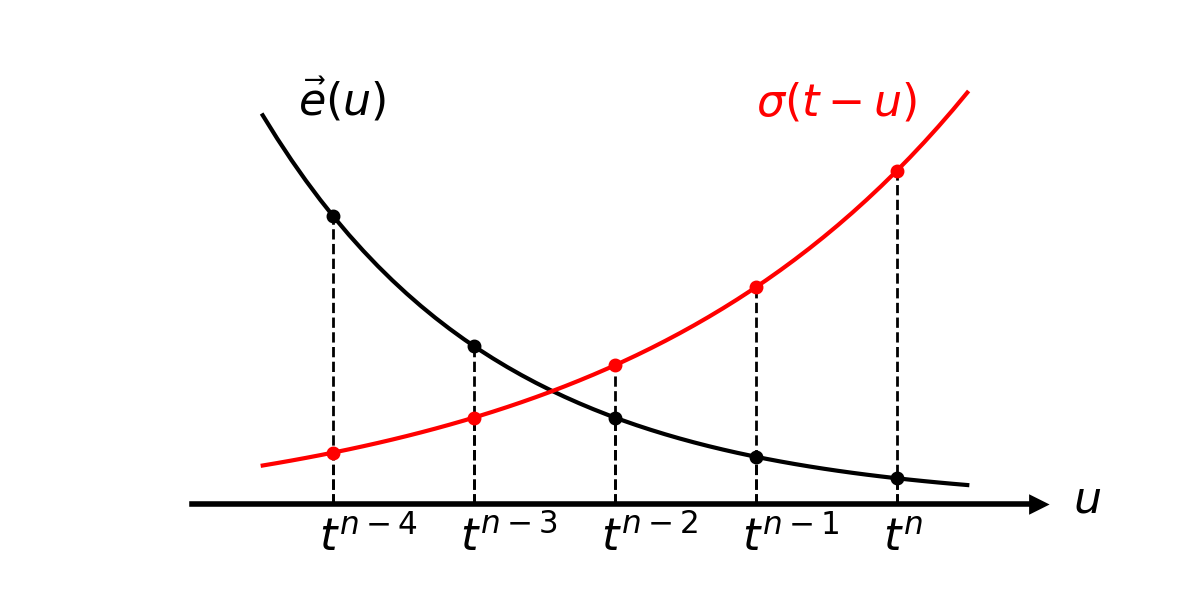
Figure 1:Conceptual diagram to describe discrete convolution process in eq. (7)
1.2Handling the singularity at ¶
The SE conductivity, at =0, is singular, whereas its integral is well-defined, as shown in eq. (6). When discretizing eq. (3), this singularity will be problematic. In particular, the issue occurs at the last time segment () of the convolution term in eq. (8), which can be written in continuous form:
This problem also occurs when the Cole-Cole function is used. Marchant (2015) (see page 31) tackled this issue by approximating at this time segment as a linear function:
Then by substituting this in to eq. (20), and evaluating the integration, the discrete form of eq. (20) is obtained:
To obtain and , we use the same trick. Integration of is not possible, so by Taylor expanding, we obtain an approximate form of which is valid for small :
By substituting eq. (23) into eq. (20) and evaluating the integral, we finally obtain
2Analytic test¶
To test the developed SimPEG-EMIP code, we compare our numerical solution with an analytic solution. A halfspace earth is assumed. The conductivity of the halfspace is 0.05 S/m and its SE parameters are: =0.7, =4ms, =0.6. Corresponding Cole-Cole parameters are: =0.8, =0.005s, =0.6. For the spatial discretization, a 2D cylindrically symmetric mesh is used; the smallest cell size is 6.5m × 5m. A horizontal source loop is located 30m above the surface. A step-off waveform is used for the input current and a horizontal receiver loop measuring the voltage (equivalent to -) is coincident with the source loop. Data are measured in the off-time over the time-range: 10-2-10 ms. Fig. 2 shows comparison between analytic and numerical solutions; they match well except for a small shift in the time of the zero-crossing, the two solutions are in good agreement.
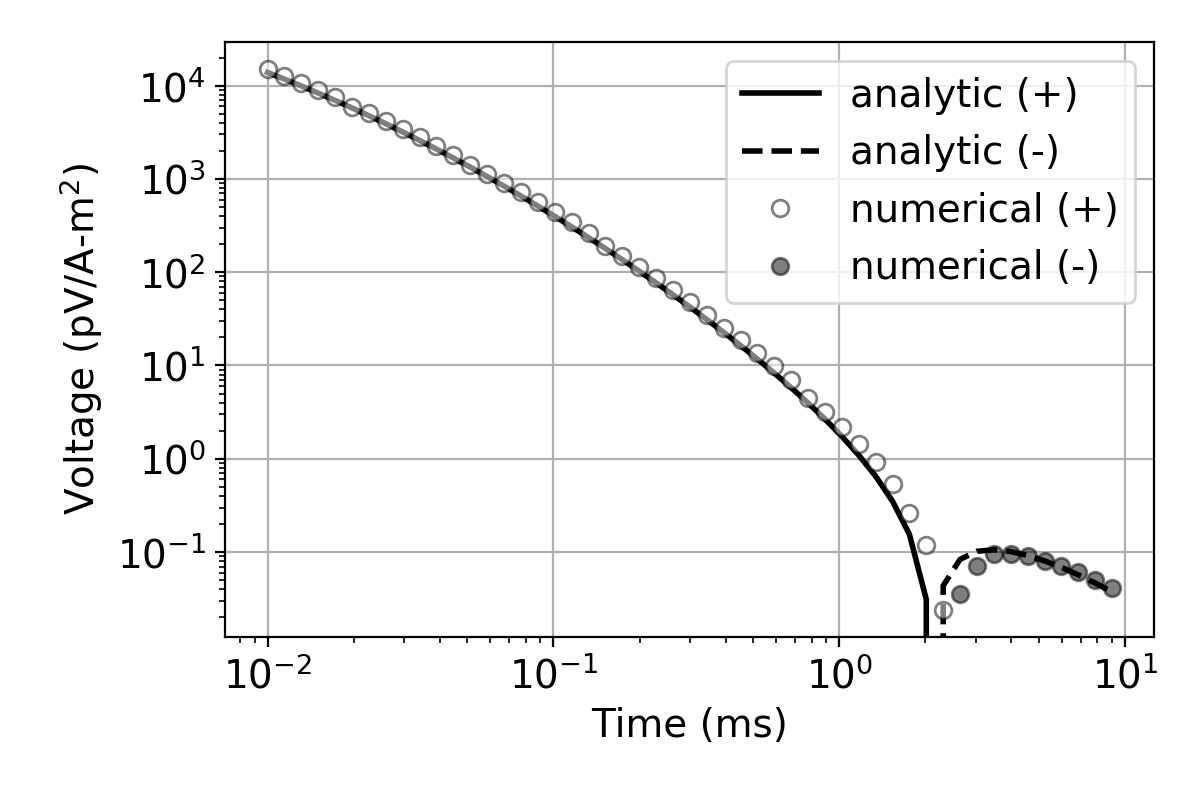
Figure 2:Comparison of numerical and analytic solutions for halfspace earth. SE parameters of the halfspace earth are =0.05S/m, =0.7, =4ms, =0.6; corresponding Cole-Cole parameters are: =0.8, =5ms, =0.6. Lines and circles distinguish analytic and numerical solutions.
Copyright © 2020 Kang et al.
- AEM
- Airborne Electromagnetics
- EM
- electromagnetics
- IP
- Induced Polarisation
- SE
- Stretched Exponential
- Marchant, D. (2015). Induced polarization effects in inductive source electromagnetic data [Phdthesis, University of British Columbia]. http://dx.doi.org/10.14288/1.0135704
- Hyman, J., Morel, J., Shashkov, M., & Steinberg, S. (2002). Mimetic Finite Difference Methods for Diffusion Equations. Computational Geosciences, 6(3), 333–352. 10.1023/A:1021282912658
- Haber, E. (2014). Computational Methods in Geophysical Electromagnetics. Society for Industrial.
